光速度不変とすると、従来の科学が前提としていた時間と空間の絶対性は崩壊せざるを得なくなった。
それまでは相対的に変化するとされていた光の速度。
アインシュタインはそれをひっくり返した。
光速度こそ絶対である。
時間と空間は光に従属するよう、コンニャクの如く可塑性に富んだものとして扱われる。
これが時間と空間の相対化である。
ケース1. ボールの場合
ここに等速度で直進中の、単車両(車両がひとつ)電車があるとする。
その車内、車両の中央に一人の人が立っている。
その人は両手に同じ大きさ、同じ重さの2つのボールを持っている。
その2つのボールを、全く同時に、電車の進行方向と、そして逆方向に投げたとする。
するとどうなるか?

車内の人は、自らが投じた2つのボールが、前後の壁に「同時」にぶつかるところを目撃する。
また、車外から静止した状態でその様子を見ている人も、ボールが「同時」に壁に当たるところを目撃する。
読者の皆様にとって、これらの事象は至極「あたりまえ」のことのように感じるだろう。
だが、この時に起こっていることを具にみていくと、事はそんなに単純ではない。
電車の進行方向に向かって投げられたボールは、空中にある間に電車が前進する分だけ、後方に投げられたボールよりも長い距離を飛ばなければならない。
しかし、このボールには、速度合成の法則により電車の速度が加わり、速度が上がるため、距離が伸びてもそれを相殺することができる。
一方、後方へ投じられたボールは、車両が前方へ進むため、より短い距離を飛ぶことになるのだが、こちらも速度合成の法則により、速度を電車の速度分減衰させられてしまう。スピードは落ちるが距離が短いので、こちらも相殺できる。
これらの力が働き、前後のボールは、車内外の観測者にとって同時に壁に到着する。
ケース2.光の場合どうなるか
ではボールではなく、光の場合はどうなるのだろうか。
ボールを持った人の代わりに、車両の中央に発光器を設置する。
車両の前後に同時に放たれた光は、車内の観測者から見ると、同時に車両の端に到達する。
では電車の外にいる観測者にとってはどうか。
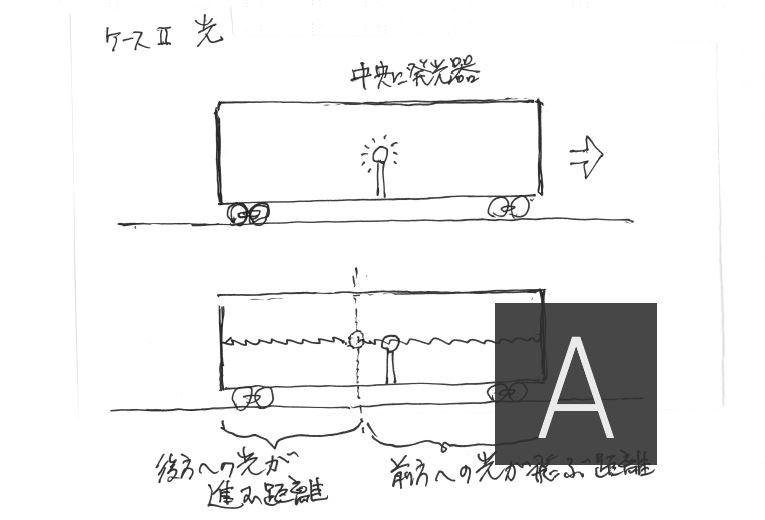
前方に進む光は、ボールの時と同様、電車が前に進んでいるのでより長い距離を進まなければならない。
また、後方へ進む光は、電車が前に進む分、短い距離を飛べばいい。
ボールのときと違うのは、光の速度は一定であるため、速度合成の法則が適用されないというところだ。
発光器から出た光には、電車の速度が加わることも、それによってスピードを減らされることもない。
従って車外から観測すると、後方へ進む光の方が、前方へ進む光よりも先に壁に到達するのである。
高速で進むと時間が遅れる
直径が30万kmほどある、滅茶苦茶巨大なロケットを想像してほしい。
「そんな巨大なロケット、素材は何で、推進力はどうやって得るんだ?」という疑問は胸にしまっておこう。
ガンダム世代なら、スペースコロニーみたいなもんをイメージするといいかもしれない。
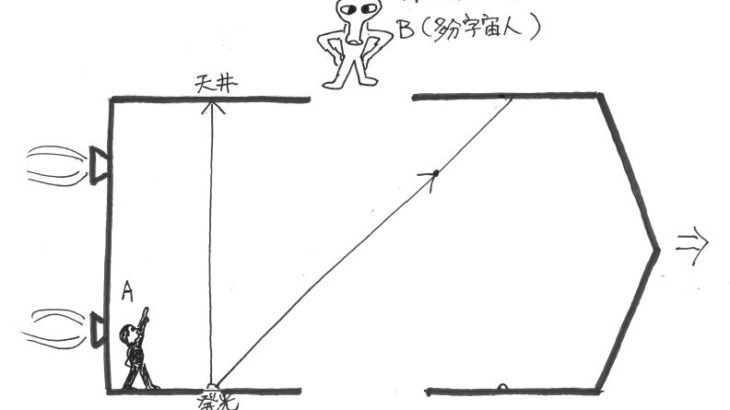
その巨大なロケットの床には発光器があり、30万キロ上にある天井に向けて光を放つ。
発光器から放たれてちょうど1秒後、光は天井に到着するはずである。
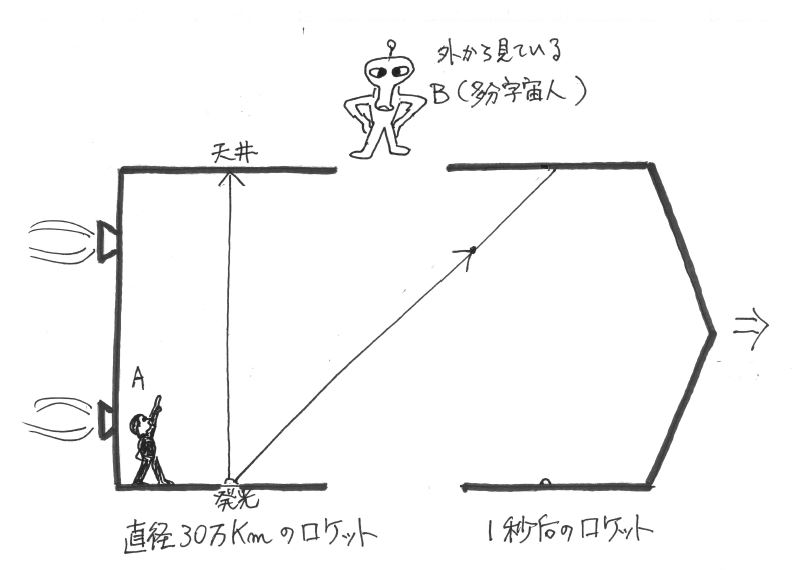
さて、このロケットが物凄いスピードで進んでいる間に、発光器から光を放つと、ロケットに乗っている観測者Aから見ると、光はちょうど1秒後に天井に届いている。
しかしロケットの外から静止してその様子を観測しているB(「ロケットの外?」という気持ちは分かるが、それも胸にしまっておいてほしい。)からは、光が発光器から出て1秒後、天井に向かって斜めに飛んでいる途中の光を目撃することになる。
いくら速いといっても、光速にだって限界はある。
光が天井に至るまでに、ロケットは前に進んでしまっているので、外から観測すると斜めに飛んでいるように見える。
そして、直進よりも、斜めの方が距離が長い(イラスト参照)。
ゆえに外から見た光は1秒では、目的地である天井に到達することはできない。
これが、高速で進むロケット内の時間が遅れる理屈であり、特殊相対性理論が語っていることである。
アインシュタインはこの考察から、同じ現象を目撃していながら観測者AとBの観測結果が異なることは問題ない、とした。
どちらの観測結果も正しいのだ。
これが「相対性理論」の「相対」の意味である。